Forschungshighlight: Molecular Dynamics on MOGON’s GPU’s

Es ist uns eine Freude Sie auf eine aktuelle Veröffentlichung aus dem Fachbereich Physik hinzuweisen, die durch die Nutzung der GPU-Knoten von MOGON möglich wurde:
"Anomalous Fluctuations of Nematic Order in Solutions of Semiflexible Polymers" von S.A.Egorov, A.Milchev, K.Binder, erschienen inPhysical Review Letters 116, 187801 (2016).
(Alternativ hier)

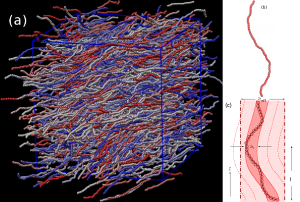
(a) (a) Snapshot of a system of semiflexible polymers with length N = 32, stiffness \(\epsilon_b = 100 \) , at concentration \(\rho = 0.6 \) (deep in the nematic phase) (b) Typical conformation of a semiflexible polymer in the nematic phase (N = 64, \(\epsilon_b = 16\), \(\rho = 0.4\). (c) Schematic description of nematic order: each chain has its own cylindrical (bent) tube of diameter \(2r_{\rho}\), defined such that it contains only monomers from the considered chain. The tube is placed inside a straight wider cylinder of diameter \(2r_{eff}\). The definition of the deflection length \(\lambda\) is indicated. — (a) Snapshot of a system of semiflexible polymers with length N = 32, stiffness \(\epsilon_b = 100 \) , at concentration \(\rho = 0.6 \) (deep in the nematic phase) (b) Typical conformation of a semiflexible polymer in the nematic phase (N = 64, \(\epsilon_b = 16\), \(\rho = 0.4\). (c) Schematic description of nematic order: each chain has its own cylindrical (bent) tube of diameter \(2r_{\rho}\), defined such that it contains only monomers from the considered chain. The tube is placed inside a straight wider cylinder of diameter \(2r_{eff}\). The definition of the deflection length \(\lambda\) is indicated.

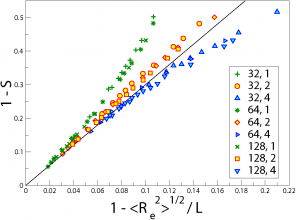
Plot of the deviation from perfect nematic order, \(1-S\), vs the relative reduction \(1 - \langle R^2_e \rangle^{1/2}/L\) of the end-to-end distance for three choices of N = 32, 64, and 128, and three choices of the \(N/\epsilon_b =\) 1, 2, and 4, as indicated. Different points with the same symbol refer to different choices of the density \(\rho\). The fully stretched chain would be the origin of the plot whereas the straight line shows \(1-S = 3\frac{\lambda}{\ell_p}\). Rigid rods would correspond to the ordinate axis here.

The nematic ordering in semiflexible polymers with contour length \(L\) exceeding their persistence length \(\ell_{p}\) is described by a confinement of the polymers in a cylinder of radius \(r_{eff}\) much larger than the radius \(r_{\rho}\) expected from the respective concentration of the solution. Large scale Molecular Dynamics simulations combined with Density Functional Theory are used to locate the Isotropic-Nematic \((I−N)\)-transition and to validate this cylindrical confinement. Anomalous fluctuations, due to chain deflections from neighboring chains in the nematic phase are proposed. Considering deflections as collective excitations in the nematically ordered phase of semiflexible polymers elucidates the origins of shortcomings in the description of the \(I−N\) transition by existing theories.